Archives de catégorie : Destination maths – collège et lycée

Destination maths - collège et lycée

L’escargot de Pythagore

Travail réalisé par Inès (4è)

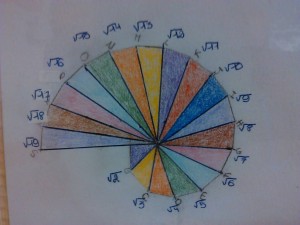
C’est une figure intéressante car elle permet de construire géométriquement les racines carrées des entiers consécutifs. On commence par représenter un triangle rectangle dont les côtés de l’angle droit mesurent 1 cm de longueur (plus petit triangle violet sur la photo). Par application de la propriété de Pythagore son hypoténuse a une longueur égale à la racine de 2 cm.

On poursuit la construction par un nouveau triangle rectangle dont un des côtés de l’angle droit est l’hypoténuse du triangle précédent, l’autre côté de l’angle droit ayant une longueur de 1 cm (on obtient le petit triangle jaune). Et ainsi de suite…

Les longueurs de l’hypoténuse des triangles successifs valent respectivement racine de 2 cm, racine de 3 cm, racine de 4 cm…

Destination maths - collège et lycée

Peut-on créer facilement une anamorphose ?

Travaux réalisés par Eléna (2nde) et par Allan (6è)

Une anamorphose est une illusion d’optique qui permet de faire en sorte qu’une image complètement déformée redevient normale quand elle est vue d’un point précis ou grâce à un «décodeur» tel qu’un miroir, une caméra ou un appareil photo.
Les anamorphoses obliques furent les premières anamorphoses créées à la fin du 15e siècle. Les exemples connus les plus anciens on été retrouvés dans les manuscrits de Léonard De Vinci.

Eléna vous propose son anamorphose oblique :

Un cube est représenté en perspective à travers un appareil photo incliné légèrement  vers la feuille de dessin :

Si on regarde  normalement le cube que l’on vient de dessiner (en se plaçant à la verticale au dessus du dessin), voilà ce qu’on verra :


Tout est une question de point de vue !

« Suite de triangles » est une œuvre réalisée en 2007 par Felice Varini. Elle est située à Saint-Nazaire. Il s’agit d’une anamorphose, ici une suite de triangles rouges, qui ne peut être vue correctement qu’à partir d’un unique point de vue.

Allan vous propose son interprétation du triangle à la manière de Varini :

La première vue permet de percevoir un triangle complet (le point de vue est parfait) ; la deuxième nous montre les deux parties du triangle.

 

 

 

 

Destination maths - collège et lycée

La grande ourse et l’étoile polaire

Activité de mathématiques  réalisée avec Morgan – élève de 6ème

La grande ourse

Cette constellation de l’hémisphère nord se repère facilement car elle contient une grande de casserole. En étendue, c’est la troisième constellation du ciel. Ses sept étoiles les plus brillantes sont observables toutes les nuits de l’année. Ce sont elles qui forment la casserole.

La Grande Ourse permet également de retrouver l’étoile polaire… la boussole de notre ciel étoilé ; utile parfois pour se repérer la nuit.

L’étoile polaire de l’hémisphère nord est une étoile visible  qui se trouve à peu près dans l’alignement de l’axe de rotation de la Terre. Depuis la Terre, elle semble immobile alors que les autres étoiles semblent décrire, pendant la nuit, un mouvement circulaire autour de l’étoile polaire.

Illustration ci-dessus : « Connaître le nord avec les étoiles » tirée du site http://montagneloisir.chez-alice.fr/guideorient.htm

Pour retrouver l’étoile polaire

On prend les deux étoiles du bec de la casserole de la grande ourse  puis on reporte cinq fois la longueur entre ces deux étoiles. On tombe sur l’étoile polaire.

Morgan a reproduit la grande ourse en partant de l’activité disponible en cliquant ici.

Destination maths - collège et lycée

Le nombre Pi

Le nombre Pi a toujours passionné les scientifiques. L’une des plus anciennes traces de ce nombre remonte à 1800 ans avant J.-C., dans le papyrus de Rhind (une des sources les plus importantes sur les mathématiques de l’Égypte antique). On lui attribuait une valeur proche de 3,26.
Sans ce nombre pas de calcul de la circonférence d’un cercle, pas plus de calcul de son aire ou encore pas de calcul du volume d’une sphère.
C’est un nombre aux décimales sans limite et sans suite logique. On appelle cela un nombre irrationnel.
Voici à quoi ressemble le début de ce nombre : 3,1415926535897932384626433832795028841971693993751058
Aujourd’hui on connaît 10 000 milliards de décimales de Pi ! Si vous voulez chercher les suivantes…

Destination maths - collège et lycée

La corde à 13 noeuds – Une découverte antique

Cette corde -appelée aussi corde égyptienne- a été très utilisée dans l’antiquité et au Moyen Âge. Elle est constituée de 13 nœuds régulièrement répartis entre lesquels on a 12 espaces égaux. La corde une fois tendue peut former un triangle constitué de 3, 4 et 5 espaces dont la particularité est d’avoir un angle droit entre ses deux côtés les plus courts.
Cette corde permettait du coup de vérifier la perpendicularité de deux « longueurs ».Certains maçons s’en servent encore aujourd’hui comme instrument de travail ; par exemple pour vérifier la perpendicularité de deux murs.

On veut prouver que le triangle 3,4 et 5 est bien un triangle rectangle. Quel théorème va-t-on utiliser ?

 

Destination maths - collège et lycée

Thalès et l’histoire de la mesure de la grande pyramide

Thalès était à la fois un mathématicien et un philosophe. Il vivait au VIème siècle avant J-C, près de la ville de Milet, sur les bords de la mer Égée, en Grèce.

L’histoire raconte que le Pharaon Amasis aurait dit que personne n’était en mesure de donner la hauteur de la grande pyramide de Guizeh … Thalès releva le défi !

Après quelques jours de voyage sur le Nil, Thalès aperçut, dressée au milieu d’un large plateau, la pyramide de Kheops. Les dimensions du monument âgé alors de 2 000 ans, dépassaient de loin tout ce qu’il avait imaginé.

Comment allait-il s’y prendre pour déterminer la hauteur de cette pyramide ?
Il regarda son ombre et eut alors cette idée :

« Le rapport que j’entretiens avec mon ombre est le même que celui que la pyramide entretient avec la sienne. »
Il en déduisit ceci : » à l’instant où mon ombre sera égale à ma taille, l’ombre de la pyramide sera égale à sa hauteur. »

Pour en savoir un peu plus sur Thalès de Milet, voir le vidéo ci-dessous :



Destination maths - collège et lycée

L’œil d’Horus et les fractions

L’œil d’Horus se dit oudjat en égyptien ce qui veut dire « complet ». Il un œil humain fardé et souligné de deux marques colorées caractéristiques du faucon pèlerin. Les Égyptiens l’utilisaient pour indiquer les fractions du hékat, unité de mesure de capacité qui servait pour les céréales, les agrumes et les liquides (un hékat valait environ 4,785 litres). C’est dans la légende des dieux Osiris et Horus qu’il faut chercher l’origine vraisemblable de cette curieuse notation.
Osiris, premier souverain de la terre d’Égypte, avec l’aide de Thot, maître suprême de l’arithmétique, de la parole et des scribes, initie les Égyptiens à l’écriture, à la science et à la magie. À l’opposé, son frère Seth, incarnation du mal, est jaloux et hait Osiris en raison de l’affection que tous lui portent. Seth tue Osiris puis s’en prend à son fils posthume Horus. Au cours d’un combat, Seth arrache l’œil gauche d’Horus, le coupe en six morceaux et le jette dans le Nil. À l’aide d’un filet, Thot récupère les morceaux mais il en manque un ! Thot le rajoute et rend à Horus son intégrité vitale.
(Texte écrit par F. Saugeon)

Mais quelle fraction de l’œil Thot doit-il rajouter pour qu’Horus retrouve un œil complet ?

Destination maths - collège et lycée

Le nombre d’or : un nombre qui fascine

1,61803398875… Ce nombre correspond à une proportion. On le désigne par la lettre grecque « Phi » en hommage à Phidias – sulpteur grec qui décora le Parthénon à Athènes.

Il est présent dans des phénomènes naturels,  par exemple dans la fleur de tournesol, dans la pomme de pin ou encore dans la coquille de certains mollusques. On le retrouve dans l’oeuvre des plus grands artistes (Vitruve, Salvador Dali ou  Léonard de Vinci). Il est aussi omniprésent dans les monuments remarquables tels que le Parthénon, Notre Dame de Paris…

Pour en savoir plus sur ce nombre, regardez la vidéo ci-dessous :

Ou encore celle-ci :